Recentemente, surgiu numa discussão a evolução da taxa de mortalidade infantil. A taxa de mortalidade infantil tem sido com grande frequência usada como principal exemplo do sucesso do Serviço Nacional de Saúde. E isto leva-me a um texto um pouco mais técnico desta vez.
É inegável o grande caminho percorrido desde os anos 60, e os anos mais recentes traduzem a estabilização desse sucesso.
Figura 1:

Nos últimos dois anos, recorrendo aos valores publicados na Pordata e com origem em estatísticas oficiais, houve uma subida da taxa de mortalidade infantil. Essa subida gerou comentários de alguma preocupação e interpretações de ser um sinal da falta de capacidade de resposta do sistema de saúde (e do Serviço Nacional de Saúde em particular), em consequência da crise económica e dos cortes de orçamento do Serviço Nacional de Saúde.
A visibilidade política e pública da taxa de mortalidade infantil justifica que a análise dos dados seja feita com cuidado.
Em concreto, uma pergunta crucial é saber se estas variações mais recentes são resultado de uma inversão de tendência ou se são flutuações normais, aleatórias, em torno de um valor estabilizado.
De um ponto de vista técnico, interessa saber se estes dois últimos anos estão dentro do intervalo de previsão que é gerado pela experiência passada.
A resposta a esta pergunta significa saber se a subida dos dois últimos anos é ou não é suficientemente elevada para em termos estatísticos se poder dizer que há uma situação anómala.
Aliás, a observação de que houve uma subida nos dois últimos anos da taxa de mortalidade infantil não pode deixar de reconhecer que o ano de 2010 foi anormalmente baixo (embora não seja estatisticamente anómalo).
Figura 2:

A consolidação dos valores conseguidos para a taxa de mortalidade infantil é obviamente um aspecto relevante do sistema de saúde português, sendo por isso fazer um seguimento próximo do indicador.
Tendo afirmado que os dois últimos anos não são substancialmente distintos, em termos estatísticos, do passado recente, os gráficos seguintes dão suporte a esta posição, calculados com base na informação da Pordata.
No primeiro gráfico é traçada a análise de regressão da taxa de mortalidade na evolução do tempo, usando uma função quadrática, e desde 1980, excluindo os anos de 2011 e 2012. Para estes dois anos, é apresentado o valor previsto e o respectivo intervalo de previsão. No segundo gráfico, é traçada a análise de regressão, iniciando-se em 2000, com um modelo linear no tempo, e novamente excluindo 2011 e 2012, apresentando o valor previsto e o respectivo intervalo de previsão. Por fim, no terceiro gráfico, considera-se um modelo em variáveis logaritmizadas, e repete-se o procedimento – exclusão dos dois últimos anos dos cálculos, sendo depois comparado o valor observado com o intervalo de previsão.
A regularidade significativa dos dois primeiros gráficos é ter os valores dos dois últimos anos dentro dos intervalos de previsão (os resultados quantitativos são apresentados em tabela no final). Mas no terceiro gráfico, o valor de 2012 sai fora do intervalo de previsão, indicando um valor fora e acima do que seria de esperar. Fica agora a escolha quanto ao modelo mais apropriado. E se o modelo da figura 3 tem melhor aderência estatística, o facto de na parte final o termo quadrático indicar um aumento da taxa de mortalidade infantil levanta dúvidas sobre a sua razoabilidade; por seu lado, o modelo com a variável logaritmizada (equivalente a ser linear em termos de taxas de crescimento) tem menor aderência estatística. Mas tomando a variável logaritmizada dá-se, de certo modo, maior importância a variações na taxa de mortalidade infantil quando esta já tem valores baixos (e em que a mesma variação absoluta da taxa significa uma variação em termos percentuais superior).
Daqui, e sem fazer mais testes estatísticos, creio que será mais adequado considerar que o valor de 2012 ainda não é estatisticamente revelador de uma alteração de tendência (preferência dada aos primeiros modelos), embora seja de seguir com atenção – a manter-se a tendência de subida por mais um ano, será um sinal de alerta a ter em conta.
Claro que quem quiser dizer que 2012 contém já esse sinal de alerta, pode usar o terceiro modelo, embora de menor qualidade de ajustamento estatístico.
Figura 3:
 Figura 4:
Figura 4:

Figura 5:

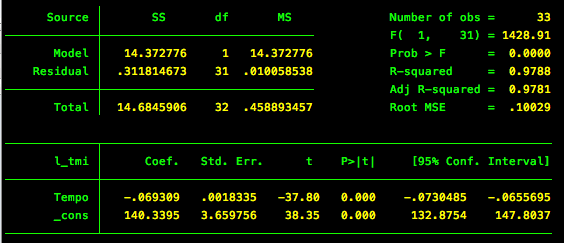
Quadros da análise de regressão: